Loss Functions

Loss Functions

Note: If you think I should correct something, let me know 😊.

This blog includes:

1. What is a Loss Function
2. When do we use Loss Function
3. Common Loss Functions (Regression)
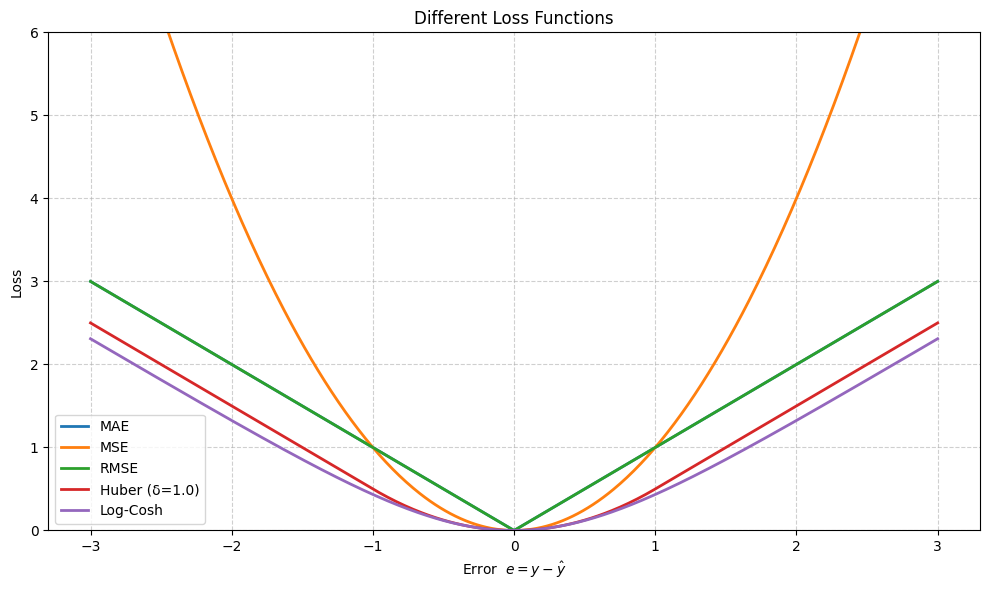
4. Mean Absolute Error (MAE)
5. Mean Squared Error (MSE)
6. Root Mean Squared Error (RMSE)
7. Huber Loss
8. Log-Cosh Loss
9. Classification Losses
10. Reconstruction / Perceptual Losses

What is a Loss Function?

A loss function (or cost function) can be regarded as a score card that tells us how far the model's prediction is from the ground truth. We train models by minimizing this loss, so a lower value indicates better predictions.

When do we use Loss Function?

• Input goes into the model → Model produces a prediction (say \(\hat{y}\)) and we have the actual value \(y\).
• The loss function compares \(\hat{y}\) with \(y\).
• The model updates its parameters via an optimizer to reduce this loss on the next iteration.

\[ L(y, \hat{y}) \]

The goal of any machine‑learning model is to minimize \(L\).

Some Common Loss Functions in Regression Tasks

1. Mean Absolute Error (MAE)

\[ L_{\text{MAE}} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| \]

\(L_{\text{MAE}}\) measures the average absolute difference between predictions and actual values — it cares only about the magnitude, not the sign.

import numpy as np

def mae_loss(y_true, y_pred):
    return np.mean(np.abs(y_true - y_pred))

2. Mean Squared Error (MSE)

\[ L_{\text{MSE}} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]

Squaring the error magnifies larger mistakes, making MSE sensitive to outliers and well‑suited for gradient‑based optimization.

def mse_loss(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

3. Root Mean Squared Error (RMSE)

\[ L_{\text{RMSE}} = \sqrt{L_{\text{MSE}}} = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 } \]

Taking the square root brings the metric back to the original scale of the target variable.

def rmse_loss(y_true, y_pred):
    return np.sqrt(mse_loss(y_true, y_pred))

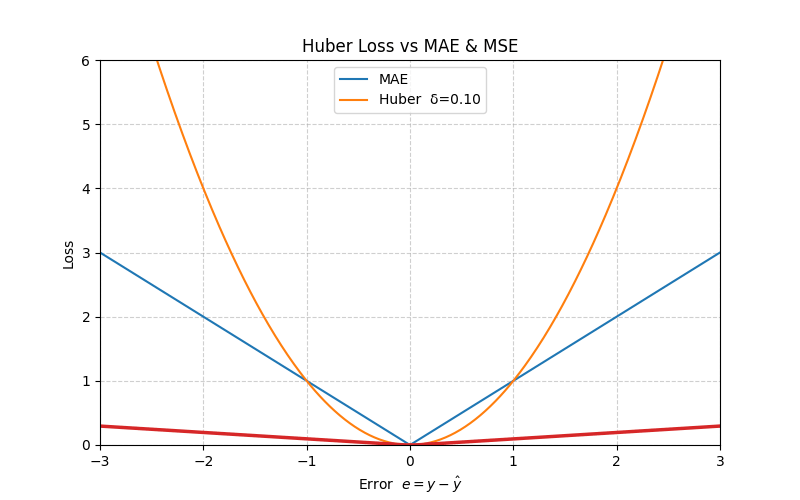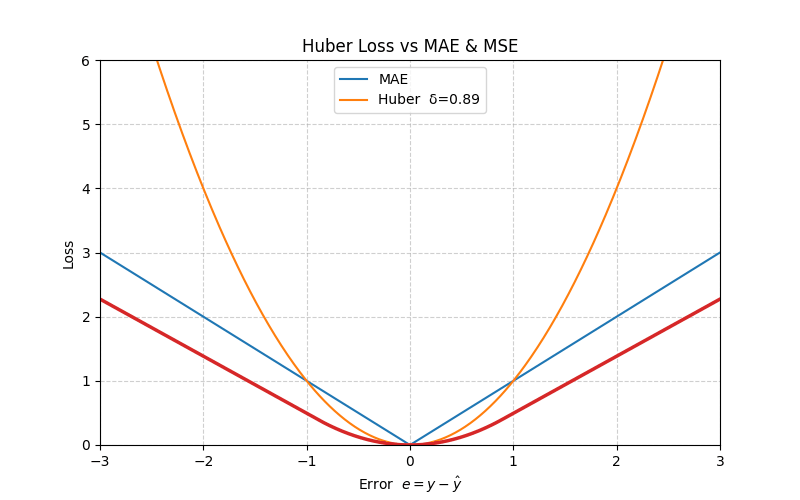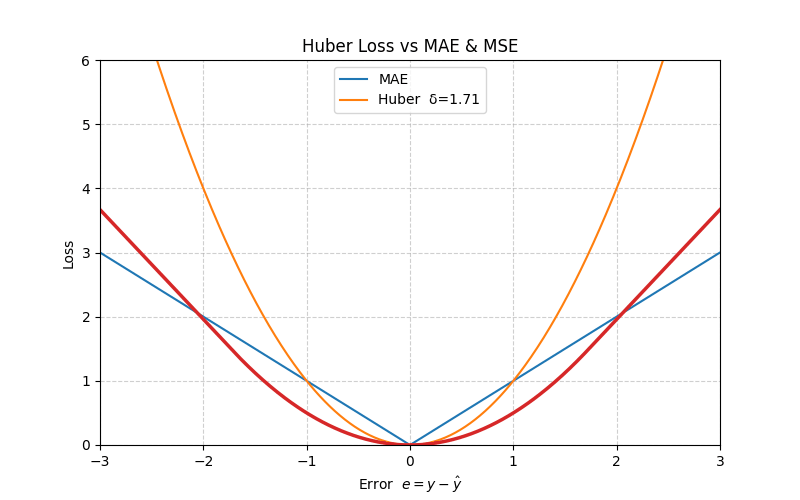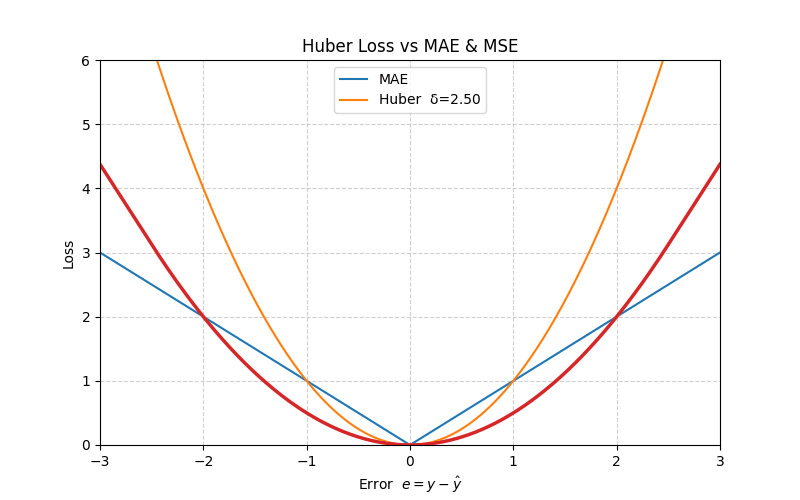
4. Huber Loss

The Huber loss blends MAE and MSE: it is quadratic for small errors (fast convergence) and linear for large errors (robust to outliers).

\[ L_{\text{Huber}}(e) = \begin{cases} \frac{1}{2} e^2, & |e| \le \delta \\ \delta \left( |e| - \frac{1}{2} \delta \right), & |e| > \delta \end{cases} \]

At \(e = \delta\), both branches meet smoothly:

\[ L_{\text{Huber}}(\delta) = \frac{1}{2}\,\delta^2 \]

Gradient:

\[ \frac{\partial L_{\text{Huber}}}{\partial \hat{y}} = \begin{cases} -(y-\hat{y}) = -e, & |e| \le \delta \\ -\delta\,\operatorname{sign}(e), & |e| > \delta \end{cases} \]

Second derivative:

\[ \frac{\partial^2 L_{\text{Huber}}}{\partial \hat{y}^2} = \begin{cases} 1, & |e| \le \delta \\ 0, & |e| > \delta \end{cases} \]

def huber(y_true, y_pred, delta=1.0):
    e = y_true - y_pred
    abs_e = np.abs(e)
    quadratic = 0.5 * e**2
    linear = delta * (abs_e - 0.5 * delta)
    return np.mean(np.where(abs_e <= delta, quadratic, linear))

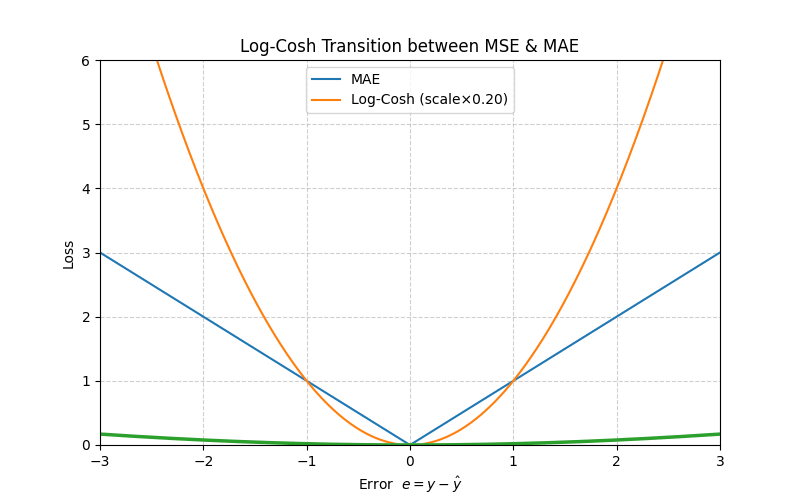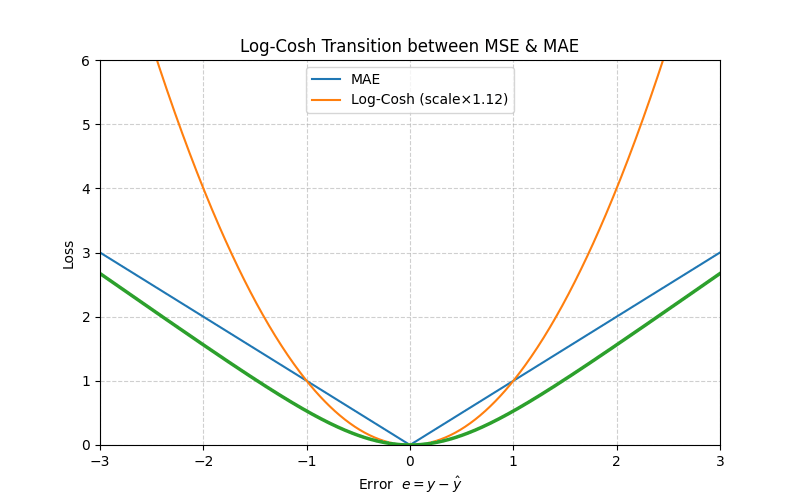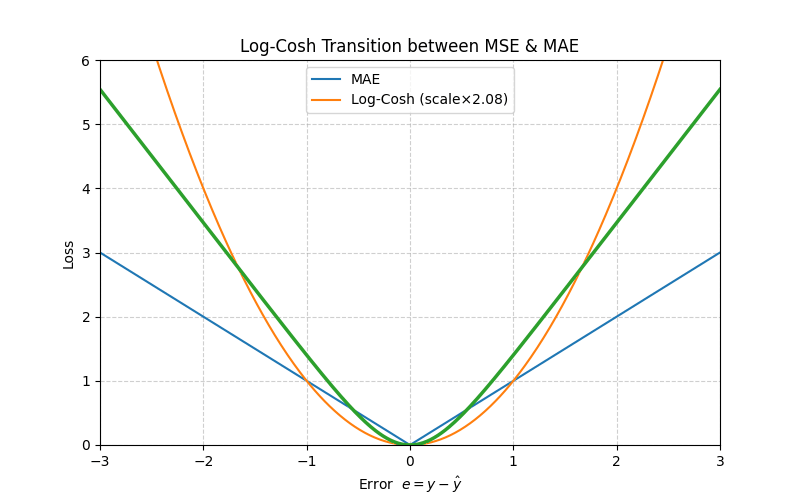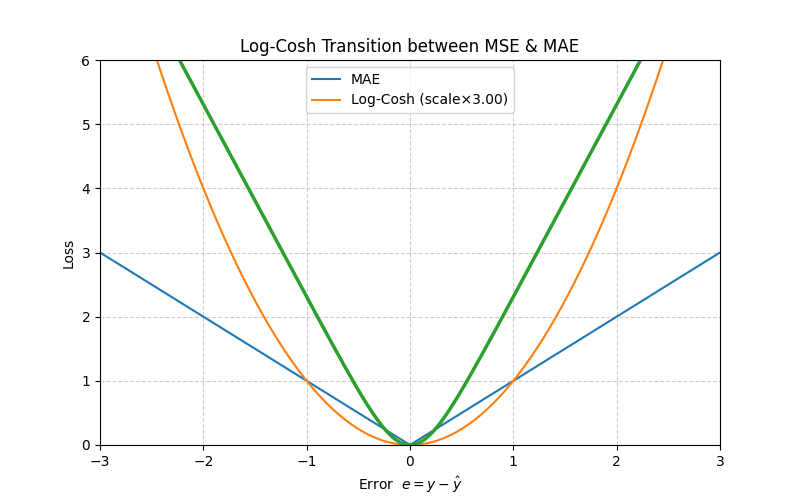
5. Log‑Cosh Loss

With \(e = y - \hat y\), define

\[L_{\text{LogCosh}}(e)=\log\bigl(\cosh(e)\bigr)\]

Series expansion (small errors)

\[\log(\cosh e)=\tfrac{e^2}{2}-\tfrac{e^4}{12}+\mathcal O(e^6)\]

≈ MSE when \(|e|\) is small.

Full gradient derivation

\[\frac{\partial L_{\text{LogCosh}}}{\partial \hat y}=\frac{d}{de}\log(\cosh e)\cdot\frac{\partial e}{\partial \hat y}\]

\[\frac{\partial e}{\partial \hat y}=-1\]

\[\frac{d}{de}\log(\cosh e)=\frac{1}{\cosh e}\cdot\frac{d}{de}\cosh e\] \[\frac{d}{de}\cosh e=\sinh e\] \[\therefore \frac{d}{de}\log(\cosh e)=\frac{\sinh e}{\cosh e}=\tanh e\]

\[\boxed{\displaystyle\frac{\partial L_{\text{LogCosh}}}{\partial \hat y}=-\tanh(e)=-\tanh(y-\hat y)}\]

Second derivative:

\[ \frac{\partial^{2} L_{\text{LogCosh}}}{\partial \hat{y}^{2}} = 1 - \tanh^{2}(e) = \operatorname{sech}^2(e) \]

def log_cosh(y_true, y_pred):
    e = y_true - y_pred
    return np.mean(np.log(np.cosh(e)))

Classification Loss Functions

When the target \(y\) is categorical, our objective is usually to maximize the log-likelihood of the correct class. Below are the most common losses.

1. Binary Cross-Entropy (BCE)

Assume each label \(y \in \{0,1\}\) is drawn from a Bernoulli distribution parameterised by the model's prediction \(\hat y = p_\theta(y{=}1 \mid \mathbf x)\). Its probability mass function is

\[ P_\theta(y \mid \mathbf x) \;=\; \hat y^{\,y}\, (1-\hat y)^{\,1-y}. \]

The log-likelihood for a single observation becomes

\[ \ell(\theta) \;=\; \log P_\theta(y \mid \mathbf x) \;=\; y \log \hat y \;+\; (1-y)\log(1-\hat y). \]

Maximising the likelihood is identical to minimising its negative, yielding the **Binary Cross-Entropy loss**

\[ L_{\text{BCE}}(y,\hat y) = -\bigl(y\log\hat y + (1 - y)\log(1 - \hat y)\bigr). \]

Gradient with respect to the probability \(\hat y\)

\[ \frac{\partial L_{\text{BCE}}}{\partial \hat y} = -\frac{y}{\hat y} + \frac{1 - y}{1 - \hat y} = \frac{\hat y - y}{\hat y(1-\hat y)}. \]

When training with logits \(z = \sigma^{-1}(\hat y)\) instead of probabilities, the derivative simplifies elegantly to

\[ \frac{\partial L_{\text{BCE}}}{\partial z} = \hat y - y, \]

which makes logistic-regression-style updates extremely convenient.

import torch.nn.functional as F

def bce_loss(y_true, y_pred, eps=1e-7):
    y_pred = y_pred.clamp(min=eps, max=1 - eps)
    return F.binary_cross_entropy(y_pred, y_true)

2. Categorical / Softmax Cross-Entropy

Let logits \(\mathbf z\in\mathbb R^{K}\) be transformed via soft-max

\[ p_k \;=\; \operatorname{softmax}(\mathbf z)_k \;=\; \frac{\exp(z_k)}{\sum_{j=1}^{K}\exp(z_j)}. \]

Assuming a one-hot ground-truth vector \(\mathbf y\) with \(y_c=1\) for the correct class \(c\), the categorical (multinomial) likelihood of a single sample is

\[ P_\theta(\mathbf y\mid\mathbf x) \;=\;\prod_{k=1}^{K} p_k^{\,y_k} \;=\; p_c. \]

The negative log-likelihood (= loss) therefore simplifies to

\[ L_{\text{CE}} = -\sum_{k=1}^{K} y_k\log p_k = -\log p_c. \]

Gradient w.r.t. each logit \(z_k\)

\[ \frac{\partial L_{\text{CE}}}{\partial z_k} = p_k - y_k. \]

The update rule is beautifully simple: subtract the one-hot vector, add the prediction.

import torch.nn.functional as F

def softmax_ce(logits, target_index):
    return F.cross_entropy(logits, target_index)

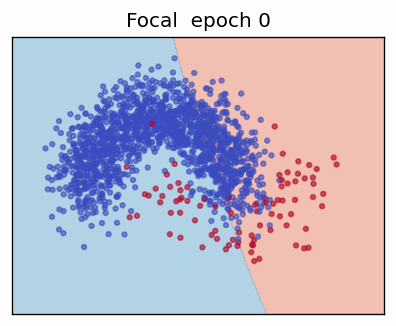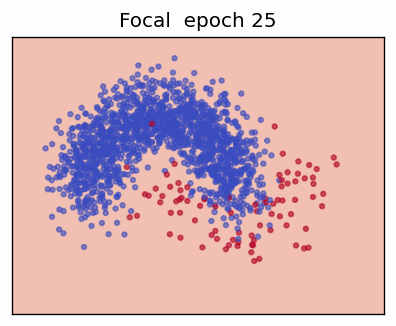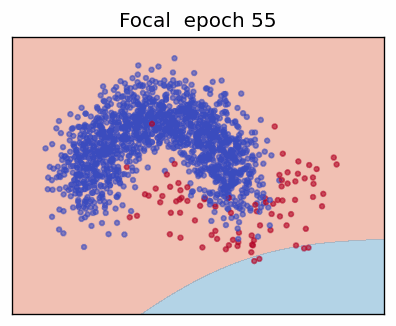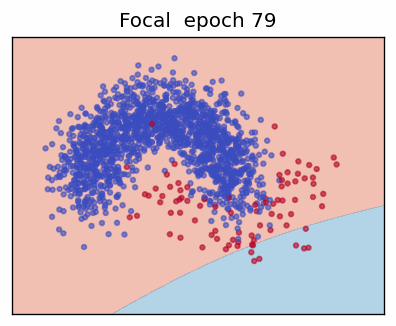
3. Focal Loss

The Focal Loss (Lin et al., 2017) adds two hyper-parameters—focusing factor \(\gamma\) and class weight \(\alpha\)—to address extreme class imbalance by down-weighting "easy" examples.

\[ L_{\text{Focal}} = -\alpha\,(1 - p_t)^{\gamma}\,\log(p_t), \quad \color{gray}{\text{where } p_t = \begin{cases} p & \text{if } y=1 \\ 1-p & \text{if } y=0 \end{cases}} \]

Gradient for the binary case

\[ \frac{\partial L_{\text{Focal}}}{\partial p} = \frac{\partial}{\partial p} \Bigl[-(1-p_t)^{\gamma}\log(p_t)\Bigr] = (1-p_t)^{\gamma-1} \Bigl[\gamma\,p_t\log(p_t) - (1-p_t)\Bigr] \cdot \begin{cases} +1 & y=1 \\ -1 & y=0 \end{cases} \]

def focal_loss(y_true, y_pred, alpha=0.25, gamma=2.0, eps=1e-7):
    y_pred = y_pred.clamp(eps, 1 - eps)
    p_t    = torch.where(y_true == 1, y_pred, 1 - y_pred)
    alpha_t = torch.where(y_true == 1, alpha, 1 - alpha)
    loss = -alpha_t * (1 - p_t) ** gamma * torch.log(p_t)
    return loss.mean()

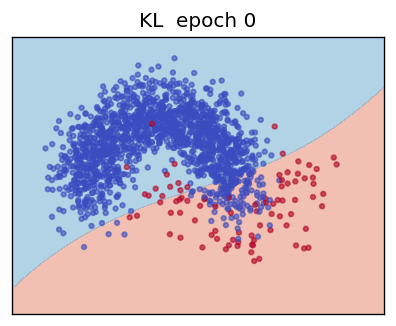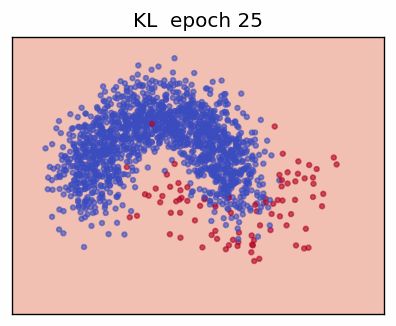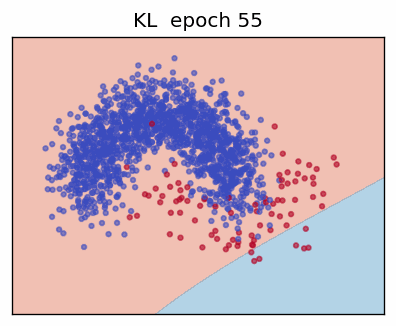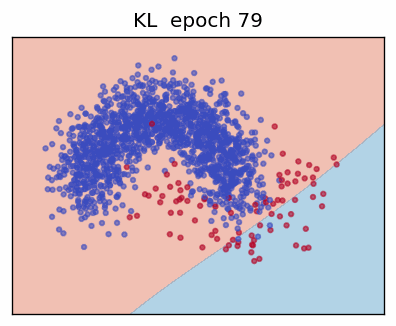
4. Kullback-Leibler Divergence (KL)

The KL divergence measures how one probability distribution \(\mathbf p\) "departs" from another distribution \(\mathbf q\). For discrete variables with \(K\) states:

\[ D_{\text{KL}}(\mathbf p\Vert\mathbf q) \;=\; \sum_{k=1}^{K} p_k \log \frac{p_k}{q_k}, \]

which can be derived by comparing the expected code-lengths assigned by two optimal Shannon codes (one built for \(\mathbf p\), one for \(\mathbf q\)). Equivalently, it is the expected excess negative log-likelihood when using \(\mathbf q\) to encode samples drawn from \(\mathbf p\).

• Non-negativity: \(D_{\text{KL}}\ge 0\) with equality iff \(\mathbf p=\mathbf q\).
• Asymmetry: \(D_{\text{KL}}(\mathbf p\!\Vert\!\mathbf q) \neq D_{\text{KL}}(\mathbf q\!\Vert\!\mathbf p)\).

Gradient w.r.t. model logits
Assume \(\mathbf q\) comes from model logits \(\mathbf z\) via soft-max. One can show

\[ \frac{\partial D_{\text{KL}}(\mathbf p\Vert\mathbf q)} {\partial z_j} = q_j - p_j. \]

This is the same form as the gradient of ordinary cross-entropy; therefore many frameworks implement KL as a drop-in replacement.

Example (Variational Auto-Encoder)
In VAEs we minimise \(\,D_{\text{KL}}\!\bigl( q_\phi(\mathbf z\mid\mathbf x) \;\Vert\; p(\mathbf z) \bigr)\), driving the approximate posterior towards the prior, while maximising the reconstruction term.

def kl_divergence(p, q, eps=1e-7):
    p = p.clamp(eps, 1)      
    q = q.clamp(eps, 1)
    return (p * (p / q).log()).sum(dim=-1).mean()

Reconstruction / Perceptual Losses

Autoencoders, VAEs, GANs and diffusion models learn to recreate the input or a target sample. Besides simple pixel-space metrics, perceptual criteria often yield crisper outputs.

1. Pixel-space L₁ (MAE)

\[ L_{L1} = \lVert \mathbf x - \hat{\mathbf x}\rVert_{1} \]

2. Binary Cross-Entropy Reconstruction

Typical for Bernoulli-likelihood VAEs where pixels are scaled to \([0,1]\).

4. Perceptual (Feature-Space) Loss

Pixel-wise criteria (L₁, L₂) often treat two images as identical if every pixel differs by a small value—even when high-level structure is clearly distorted to the human eye. Perceptual loss fixes this by comparing images in the activation space of a pretrained vision network (VGG-19, ResNet-50, CLIP ViT, …).

\[ L_{\text{percep}}(x,\hat x) \;=\; \sum_{\ell\in\mathcal L} \lambda_\ell\; \bigl\lVert \,\phi_\ell(x)\;-\;\phi_\ell(\hat x)\, \bigr\rVert_1, \]

where \(\phi_\ell\) extracts the feature map at layer \(\ell\) and \(\lambda_\ell\) are user-defined weights (often all 1).

• Super-resolution / deblurring – encourages sharp edges that "look" realistic rather than simply low MSE.
• Style-transfer – combine a content perceptual term with a Gram-matrix style term.
• GANs & Diffusion – perceptual fine-tuning leads to crisper outputs.

Back-propagation: Gradients flow through the frozen feature extractor: \(\displaystyle \tfrac{\partial L}{\partial \hat x} = \sum_\ell \lambda_\ell\, \partial \phi_\ell^\top\, \operatorname{sgn}\bigl[\phi_\ell(\hat x)-\phi_\ell(x)\bigr]\), making training stable because \(\phi_\ell\) parameters remain fixed.

import torch.nn.functional as F
from torchvision import models

vgg = models.vgg19(weights=models.VGG19_Weights.DEFAULT).features.eval()

def perceptual_loss(x, x_hat, layers=(8, 17)):  # conv3_3 ≈ 16, conv4_3 ≈ 25
    with torch.no_grad():
        feats_x, feats_hat = [], []
        out_x, out_hat = x, x_hat
        for i, layer in enumerate(vgg):
            out_x  = layer(out_x)
            out_hat = layer(out_hat)
            if i in layers:
                feats_x.append(out_x)
                feats_hat.append(out_hat)
    loss = sum(F.l1_loss(fh, fx) for fx, fh in zip(feats_x, feats_hat))
    return loss

5. Charbonnier (Smooth L1) Loss

The Charbonnier loss—sometimes called "Smooth L1"—is a strictly differentiable approximation of the absolute-error (L₁) that behaves quadratically near zero and linearly in the tails, providing robustness against outliers without the gradient singularity of L₁.

\[ L_{\text{Charb}}\bigl(e\bigr) \;=\; \sqrt{e^{2} + \epsilon^{2}}, \qquad e = x - \hat x, \]

where \(\epsilon>0\) is a small constant (e.g. 1e-3 or 1e-6) controlling the transition width between the quadratic and linear regimes.

Near zero error. Using a second-order expansion (\(e\ll\epsilon\)):

\[ L_{\text{Charb}} = \epsilon\, \sqrt{1 + \bigl(e/\epsilon\bigr)^2} \;\approx\; \epsilon \Bigl[1 + \tfrac12(e/\epsilon)^2 - \tfrac18(e/\epsilon)^4 + \dots\Bigr] \;\approx\; \tfrac{e^{2}}{2\,\epsilon} + \mathcal O(e^{4}), \]

hence the loss is effectively **quadratic** near the optimum, leading to smooth convergence.

Gradient.

\[ \frac{\partial L_{\text{Charb}}}{\partial \hat x} = -\frac{e}{\sqrt{e^{2} + \epsilon^{2}}}. \]

As \(|e|\rightarrow\infty\) this gradient approaches \(-\operatorname{sign}(e)\), matching MAE's clipping behaviour and preventing exploding updates.

import torch
import torch.nn.functional as F

def charbonnier_loss(x, x_hat, eps=1e-6):
    diff = x - x_hat
    loss = torch.sqrt(diff * diff + eps * eps)
    return loss.mean()